一、泛音的来源——驻波

0.  声场基础理论

乐器发声都是通过稳定驻波的形成来实现的。模型发声原理是，手拍击管口引起空气粒子振动，激起声波。声波在管中传播，并在两侧管口发生反射，管内存在的所有入射波与反射波叠加形成一系列稳定的具有特定频率的驻波，因而发出声音。下面将推导模型中形成的驻波的频率表达式。

声场可以由声压(逾压)p、媒质质点振动速度v和媒质密度的变化量来表征。理想声场满足运动方程,连续性方程和物态方程，其中，为媒质中的声速。

联立上述三式求得空气中声压的三维波动方程：

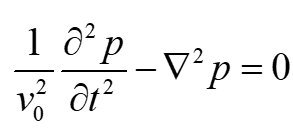
声压求出后并由运动方程可以求出质点振动速度v。

在绝热近似下，可以导出声速的表达式为

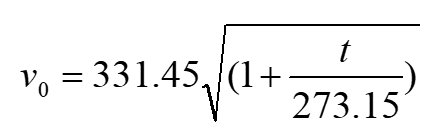
其中t是温度，单位为℃。

1.  驻波的概念

        驻波 （standing wave） 是频率相同、传输方向相反的两种波，沿传输线形成的一种分布状态。其中的一个波一般是另一个波的反射波。

2.  驻波形成的条件

 ①需要有两个固定的节点，在弦乐器上，弦必然是被张在乐器上的，两个节点很显然已经具备；

 ②两种波的频率、传输速度完全相同，但方向相反

3.  驻波的计算

3.1 波动方程

牵扯到一些计算过程，简单记录一下

若一个波源的振动方程为

则在x处其振动方程为

再利用 ，可将振动方程整理为

这里得到的是一个沿x正向传播的波动方程，不难得到沿x负向传播的波动方程为

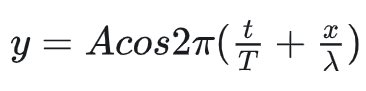
3.2 驻波的叠加

若存在如上两个频率相同，传播速度相同，反向相反的波

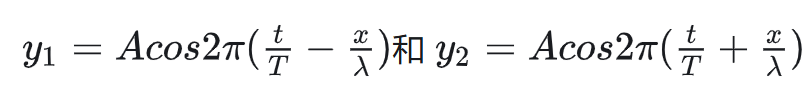
则经过叠加后的波动方程为

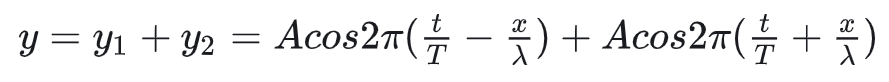
经过三角函数的和差化积后，可整理为

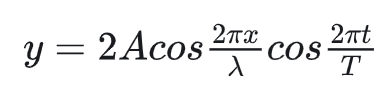
同时我们可以发现时间和位置两个变量已经被我们分离开了，这时只要研究位置部分即可。

二、泛音列的原理

1.  泛音列的产生

由上述关系可以看出，满足的点，振幅始终为0，被称为节点，相邻两个节点间的距离很显然为 ，任意两个节点之间的距离则为  ,弦乐器的两个端点必然是节点，所以弦长应符合 。

1.1 弦长关系

当 𝑛=1 时， ，此时即我们通常说的全弦振动，那么从 𝑛=2 开始，陆陆续续仍有分段的振动，图示如下：

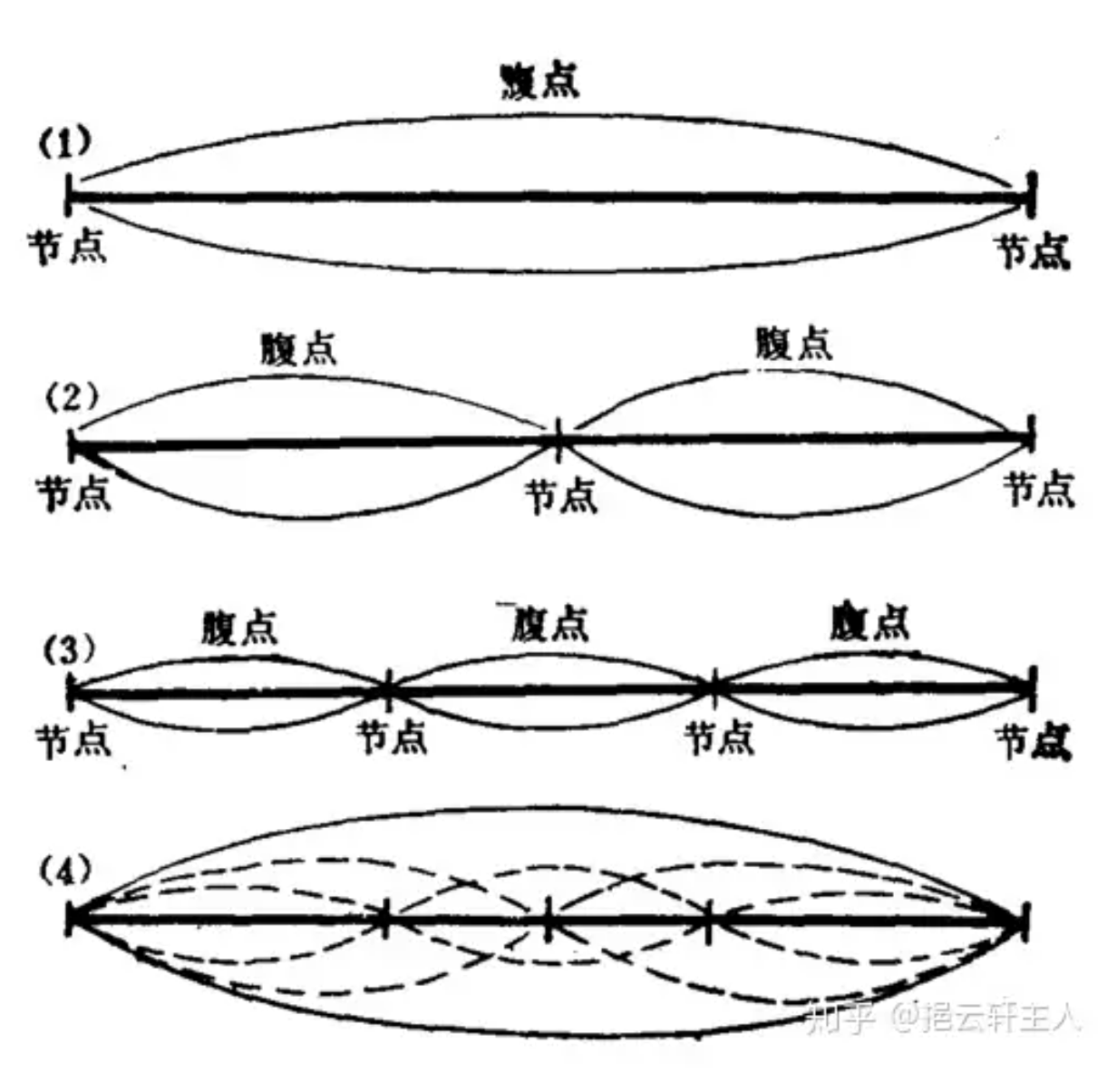
1.2 倍音

从实际出发，当一根弦在振动时，它的1/2、1/3，已经所有的1/n的振动依旧存在，这个全弦的音事实上就是一个混合音，律学上通常把n=1时的音叫做“基音”，其他的音叫做“n倍音”，这样形成的一组音叫做“泛音列”，也称为“倍音列”。泛音列是律学生律的基础。

2.  泛音的产生

从上面的叙述中，就知道了，全弦振动时有很多倍音，当我们用手在1/2处轻点时，很显然只能留下1/2处的振动（当然1/4、1/8等处的振动依然存在），这是过多的倍音被消除，只留下了高八度的二倍音，这也就是演奏时实现泛音的方法。

三、泛音列与生律

1.  弦长与音高的关系

简单来说，弦长之比与振动频率呈反比，而振动频率又与硬搞呈正比，因此简单来说，振动弦长越短，那么对应的音高也就越高。

2.  三倍音和五度相生律

三倍音与二倍音的频率之比是3/2，从听感上来说，这两个音之间成纯五度关系。因此通过纯五度关系连续生律得到的律制，都归属与五度相生律，这里包括了中国的“三分损益法”，以及西方的“毕达哥拉斯律制”

3.  五倍音和纯律

五倍音与四倍音的频率之比是5/4，从听感上来说，这两个音之间成大三度关系（当然这是纯律大三度）。在五度相生的关系上，又加入大三度关系生律，这样形成的律制，都应当归属于纯律。在琴律上，一个十分值得讨论的问题，就是古琴上是否有自发应用纯律。

来源：挹云轩琴律学习笔记之一——泛音列 - 知乎 (zhihu.com)